
Movimento sinusoidale
Calcolo di cilindri idraulici, cilindri oscillanti
La più semplice oscillazione armonica sinusoidale di un asse del cilindro regolato è un'estensione e una retrazione ciclica dello stelo pistone. Ma anche profili di movimento completamente irregolari possono essere descritti matematicamente, ponendo alla base un movimento sinusoidale in ogni punto.
Il calcolo semplificato integrato nel configuratore di prodotti HäKo (cilindro di prova >> dimensionamento idraulico) serve per il dimensionamento di un movimento dinamico in funzionamento sinusoidale. In questo caso vengono presi in considerazione soprattutto i dati del cilindro, mentre altre parti rilevanti per il sistema, come ad esempio i tubi flessibili o le valvole e le loro perdite, non vengono incluse.
Il movimento sinusoidale è definito dall'immissione di ampiezza e frequenza. In questo modo, il calcolo determina i rispettivi valori massimi del movimento, che però non si verificano contemporaneamente in caso di oscillazione sinusoidale. Ad esempio, la velocità ha il suo valore massimo nel momento in cui il valore dell'accelerazione è zero.
Per determinare le dimensioni del cilindro, questo è sufficiente per un dimensionamento tipico.
Questo calcolo non sostituisce la simulazione del sistema idraulico completo, che è necessaria in casi particolari, ad esempio quando il sistema raggiunge i suoi limiti di progettazione.
Il calcolo serve per il dimensionamento di un movimento in funzionamento sinusoidale. Non comprende il comportamento all'accensione o allo spegnimento dell'impianto idraulico.
Calcolo della forza
La forza del cilindro Fb alla pressione di esercizio è la forza che si ottiene nel funzionamento dinamico. Per pressione di esercizio si intende la pressione effettiva pb presente nella camera del cilindro, che si stabilisce a valle della valvola di controllo.
Fb = pb • A
con la superficie efficace del pistone derivante dall'alesaggio D2K e dal diametro dello stelo pistone d2s
A = π / 4 • (D2K - d2s)
La forza del cilindro Fs alla pressione di sistema è la forza che si ottiene nel funzionamento statico. Per pressione di sistema si intende la pressione ps presente a monte della valvola di controllo, che viene fornita dal gruppo.
Fs = ps • A
Movimento sinusoidale dinamico
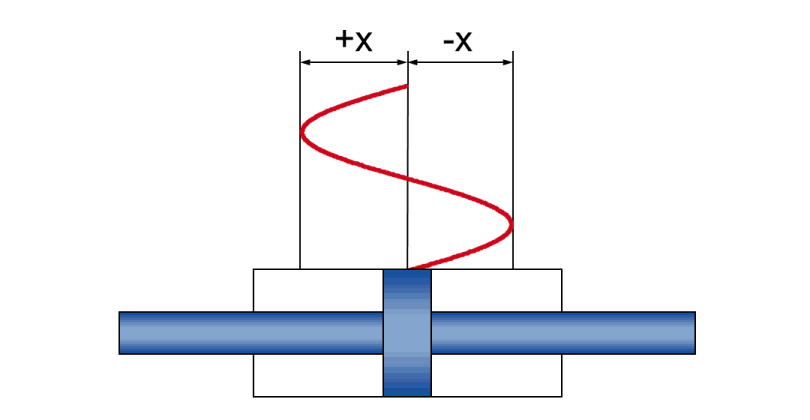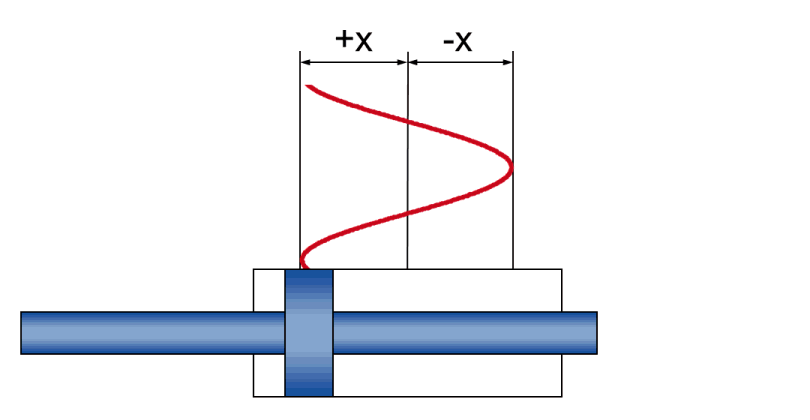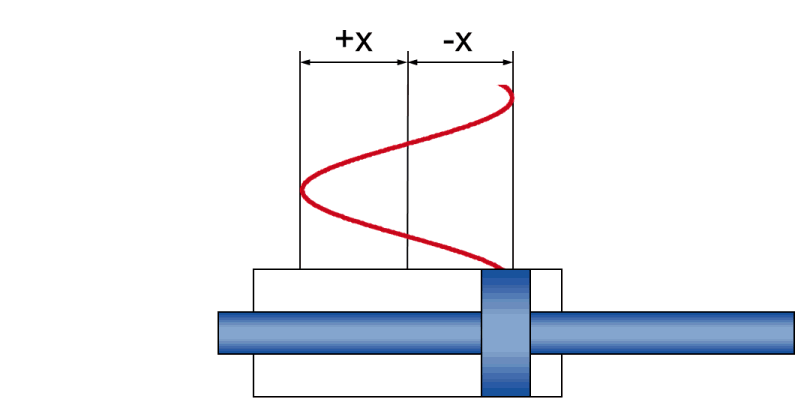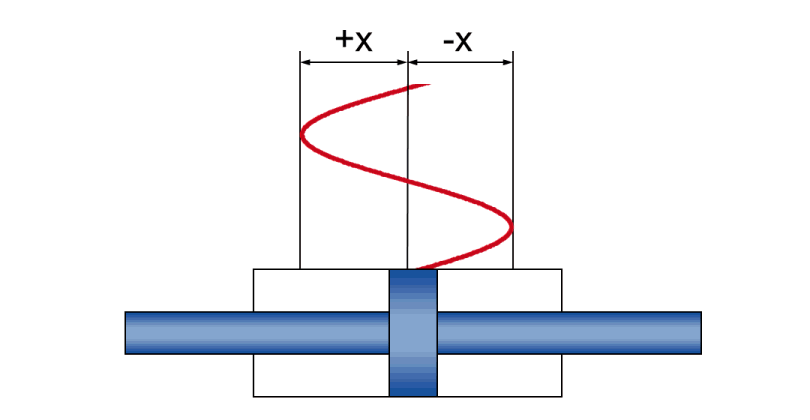
Nel funzionamento dinamico, in caso di movimento sinusoidale, si creano correlazioni fisiche tra
- Ampiezza +/- x - il movimento effettivo della corsa durante l'oscillazione
- Velocità v - la velocità pistone istantanea (e in costante variazione durante l'oscillazione)
- Accelerazione a - l'accelerazione del pistone istantanea (e in costante variazione durante l'oscillazione)
- Frequenza f - la sequenza temporale del movimento della corsa, indicata come numero di oscillazioni per unità di tempo
| Valori massimi |
| v = 2 π f x |
| a = 4 π2 f2 x |
Da ciò si ricava la portata volumetrica Q massima necessaria per il movimento
Q = v • A
con la superficie efficace del pistone A
A = π / 4 • (D2Pistone - d2Stelo)
e la forza di accelerazione Fa che il cilindro deve fornire
Fa = m • a
Dall'accelerazione massima qui calcolata e dalla massa in movimento si ricava una forza di accelerazione che il cilindro deve applicare. La massa propria dello stelo pistone è considerata nel programma di calcolo, le masse in movimento aggiuntive devono essere indicate nel campo corrispondente.
Raccomandazione servovalvola
La pressione di sistema ps si calcola tenendo conto della caduta di pressione Δp nella valvola di controllo:
pb = ps - Δp
La caduta di pressione della valvola di controllo viene solitamente indicata con 70 bar o 10 bar alla portata nominale per le servovalvole. In esercizio, tuttavia, dipende dalla portata volumetrica effettiva.
Il programma, in base alla portata volumetrica richiesta, propone una portata nominale per una possibile valvola di controllo. Per questa viene poi calcolata anche la caduta di pressione. In questo modo si dovrebbe ottenere rapidamente una panoramica della classe di grandezza della valvola necessaria.
Alla portata volumetrica calcolata deve essere aggiunta la portata volumetrica di perdita del sistema di guarnizione e della servovalvola.
Questa progettazione non pregiudica una precisa determinazione e dimensionamento della valvola.
Altre formule di calcolo per la progettazione di cilindri idraulici:
Formule di calcolo per la progettazione di cilindri idraulici
Calcolo delle velocità dell'olio ammissibili
Calcolo della resistenza all'instabilità dei cilindri idraulici
Calcolo dei casi di inflessione - Fissaggi di stelo pistone e cilindro